Corrections Applied

Spheroidal distance height correction

The height correction for distances is for the purpose of reducing terrain-height distance observations to the surface of the spheroid since spheroidal distances are required for computations on a projection. The following diagrams represent the different cases of a standard Transverse Mercator projection (Figure 1) and a special-area Transverse Mercator projection (Figure 2):

In a standard (Transverse Mercator) projection, the projection plane approximates the surface of the spheroid where the Central Scale Factor compensates only for the difference between the planar and spherical surfaces relative to the current distance from the Central Meridian. The CSF is normally 0.9996 at the central meridian, passing through exactly 1.0 where the plane cuts the spheroid, then increasing greater than 1.0 towards the edges of the zone.

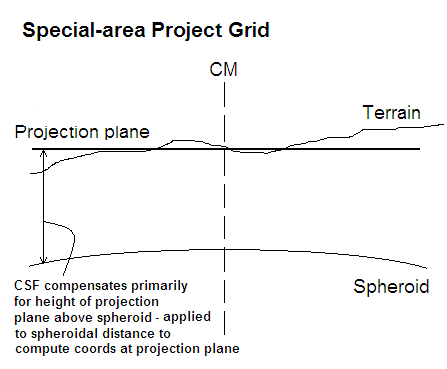
A special-area projection is typically defined for engineering purposes within a limited area and often with a restricted height range. In contrast to a standard Transverse Mercator projection, the projection plane for a special-area project grid may be defined to be at an appropriate average height for the zone and the central scale factor is set such that it primarily compensates for the average height of the projection plane above the spheroid. To simplify computations, measured distances at terrain height can be used without correction to compute plane coordinates, and conversely, a plane distance derived by simple geometry from computed coordinates will yield an approximate set-out or ground distance, and provided that all operations are within the defined horizontal and vertical extents of the projection zone, computations will be within a pre-defined tolerance. Geoida can improve the accuracy obtained by computing both coordinate and inverse values on the special-area Transverse Mercator projection. Correction of observed distances measured at terrain height must therefore be made to reduce the measurements to the height of the spheroid, and inverse distances derived from projection coordinates must likewise be raised to terrain height for set-out purposes.

Thus for both standard projections and special-area projections, correction of distances between terrain and spheroid is required for projection computations. Height correction of distances will usually be applied for this purpose by default (Reduce dists to spheroid options) but these can be over-ridden by the user if ever necessary, for example, if measured distances have already been corrected for height above the spheroid prior to entering observations into Geoida.

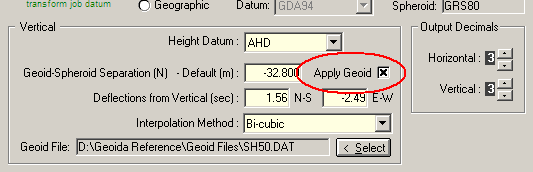
Where a geoidal height datum is used (for example, one which is related to the geoid by gravimetric spirit levelling with reference to mean sea-level, i.e. orthometric), it is necessary to incorporate geoid-spheroid separation into the correction to derive a correct distance on the spheroid. For either spheroidal or geoidal height datums, any offset from the vertical datum must also be incorporated.

Thus the corrected (horizontal) spheroidal distance is given by :

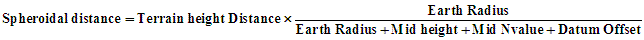
Where an orthometric (or geoidal) height datum is used, if the Apply to obs check box in Job Configuration (refer to Figure 1) was uncrossed (either by mistake or intentionally), the geoid-spheroid separation would be omitted from the correction and would yield a geoidal (or sea level) distance which may only approximate the spheroidal distance. However, the effect of its exclusion will usually only be relevant to lines over several kilometres in length and where N is very large. For a job configured with a geoidal height datum, the correct (i.e., normal) setting for the Apply to obs check box is crossed.

Refer to Geoid-Spheroid Separation for more information regarding geoid-spheroid separation.

Return to Section Titles

Curvature/refraction correction

If selected, the correction is made for all one-way observations by applying it to the observed vertical angle or the vertical component as the case may be :

Return to Section Titles

Eccentricity and non-tilting prisms correction

During the processing of SDR data, the prompt Is reflector tilting type ? is displayed where the SDR Mounting Type option (Type 01 data record) specifies that the instrument used was either (i) a telescope mounted EDM, or (ii) a standards mounted EDM where instrument and prism offsets were unequal.

If a non-tilting reflector was used, the correction is made as follows :

(i) telescope-mounted EDM

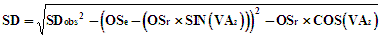
(ii) standards mounted EDM

For manually-entered traverse or radiation data where a tilting prism and telescope-mounted EDM were used, leave both EDM and Prism Offsets fields blank or set to zero. For a standards-mounted EDM with a non-tilting reflector, the eccentricity correction is zero if both offsets are equal - hence may be left blank in that case. A correction is required for a telescope-mounted EDM used with a non-tilting prism, regardless of offset values. Eccentricity correction can usually be ignored unless high accuracy is required.

Return to Section Titles

Gravitational deflection from vertical

Gravitational corrections are applied to various observation types in the Least Squares Network Adjustment option only. However if a geoid model is available at the time ANY survey computations are being made, the geoid-spheroid separation and deflection values will always be interpolated for any new or re-calculated point. Deflection corrections are applied to horizontal angle, direction, azimuth or vertical (zenith) angle observations if Correct for Gravity Deflections is ticked on the Least Squares Network Adjustment General tab.

Return to Section Titles