
Geoida
Help

|
Geoida |
Spheroid |
This option is used to define the parameters for a spheroid (or ellipsoid - see Spheroids, Ellipsoids and the Geoid below) and to display the details of all spheroids currently defined in the Definitions library.
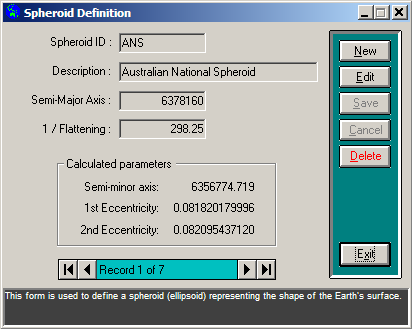
|
|
More Info: |
When Geoida is running, details of the purpose and use of each control in this window will be displayed in the bottom panel when the mouse is passed over any active object. |
Spheroid and Ellipsoid are terms used to describe the idealised geometrical shape of the Earth for mathematical purposes. Many geodesists, geophysicists, cartographers and other scientists use these terms interchangeably although usually preferring the use of one term above the other. Meanwhile others emphatically insist that there are important differences between them that should not be diminished.
However the shape of the Earth is much more complex than either of these terms represent, hence the term Geoid describes the physical shape of the Earth as being a surface of equal gravitational potential along which the direction of the gravitational attraction is always perpendicular to it. The geoid coincides exactly with the mean sea level surface of the Earth (if it were at rest) but undulates as affected by gravitational anomalies and concentrations due to continental land masses, mountains, valleys and depressions, both on the land and under the sea.
Within the Geoida software application and this Help documentation the user may find either of the terms Spheroid or Ellipsoid used and should consider them as synonymous. The following comments and definitions of the terms Spheroid, Ellipsoid and Geoid from different sources may be of interest.
|
The distinction is made between a spheroid and an ellipsoid because these terms are often used interchangeably in geodesy texts. According to the Oxford English Dictionary (OED, 1989), a spheroid is:
'An updated explanation of the Geocentric Datum of Australia (GDA) and its effects upon future mapping' - Dr Will E. Featherstone MAIC, School of Spatial Sciences, Curtin University of Technology, Circa 1995 http://www.cage.curtin.edu.au/~will/datum.html |
| Spheroid, Ellipsoid, and Geoid Spheroid is a solid generated by rotating an ellipse about either the major or minor axis Ellipsoid is a solid for which all plane sections through one axis are ellipses and through the other are ellipses or circles. If any two of the three axes of that ellipsoid are equal, the figure becomes a spheroid (ellipsoid of revolution). If all three are equal, it becomes a sphere. Geoid is the equipotential gravity surface of the earth at mean sea level. At any point it is perpendicular to the direction of gravity. 'Introduction to Geodesy: The history and concepts of modern geodesy' - Smith, James R., John Wiley & Sons, 1997. http://elearning.algonquincollege.com/coursemat/viljoed/gis8746/concepts/geodesy/spheroid.htm |
| More complicated figures The possibility that the Earth's equator is an ellipse rather
than a circle and therefore that the ellipsoid is triaxial has been
a matter of scientific controversy for many years. Modern
technological developments have furnished new and rapid methods for
data collection and since the launch of Sputnik
1, orbital data have been used to investigate the
theory of ellipticity. A second theory, more complicated than triaxiality, proposed
that observed long periodic orbital variations of the first Earth
satellites indicate an additional depression at the south pole
accompanied by a bulge of the same degree at the north pole. It is
also contended that the northern middle latitudes were slightly
flattened and the southern middle latitudes bulged in a similar
amount. This concept suggested a slightly pear-shaped Earth and was
the subject of much public discussion. Modern geodesy tends to
retain the ellipsoid of revolution and treat triaxiality and pear
shape as a part of the geoid figure: they are represented by
the spherical harmonic coefficients C22, S22
and C30, respectively, corresponding to degree and order
numbers 2.2 for the triaxiality and 3.0 for the pear shape. WAPedia: 'Figure of the Earth' |
| Converted from CHM to HTML with chm2web Standard 2.85 (unicode) |